Concert pitch, what is that?

The concert pitch, also called tuning pitch and normal pitch, is a pitch defined as a common reference point to which the instruments of a music group are tuned at the same pitch. The pitch of the commonly used concert pitch A is middle A (a′ also a1) according to multiple definitions in music history today.

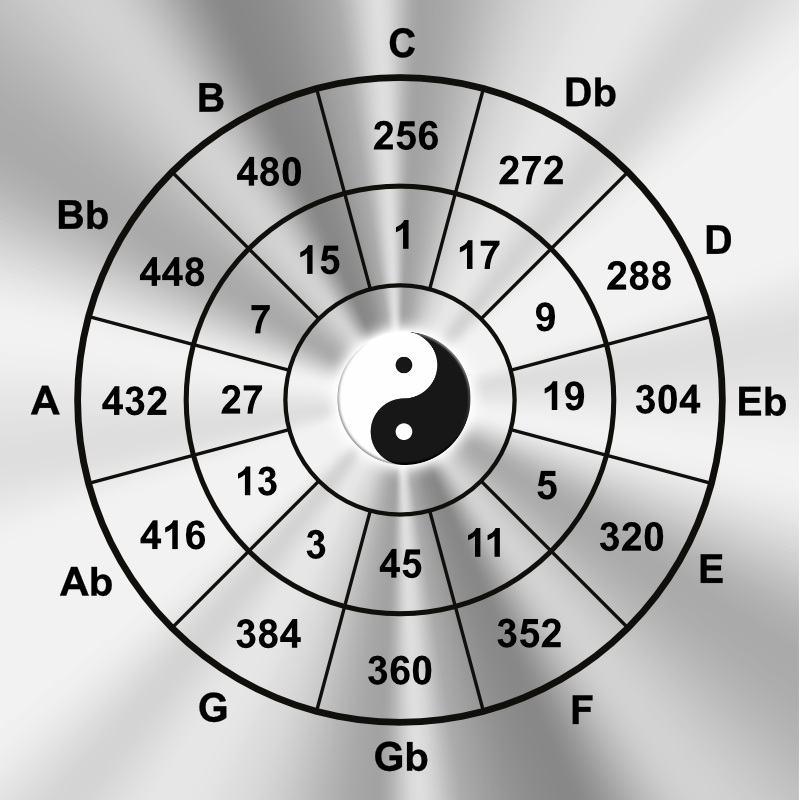
In the mainstream, this tone has a frequency of 440 hertz. It’s different with Maria Renold: this middle A (A4 in keyboard German) has a frequency of 432 Hz.

But it’s not her concert pitch. Or is it? Yes, yes, it is also her concert pitch. It has two: 128 Hertz (C3) and 432 Hertz (A4).

It works like this: she developed a scale called THE SCALE OF FIFTHS or Maria Renold tuning.
And that’s where these two frequencies come in.

Then there is the Pythagorean tuning, where these two chamber tones also occur.

And then there is just intonation with a reference frequency of 15 hertz .

Well, you can see that the term concert pitch doesn’t just stand for a frequency.

How did this term come about, what is the history? Read here!

I knew 128 hertz before I found out that frequency played a role in Maria Renold and Rudolf Steiner. 

That came about because I calculated the world of musical frequencies mathematically and physically from the ground up.
Steiner and Renold could not do that.
They didn’t think of it and they didn’t have a computer with Excel spreadsheets. And it wasn’t Maria Renold’s intention at all.

Rudolf Steiner, it seems he said C=256 Hz, which is actually the same in frequency, because 256 Hz is an  octave  of 128 Hz. And 128 Hz is an octave of 1 Hz!
The number 1 appears in all cultures as a source that contains in germ the latent qualities of all possible planes of being.

That’s how it happened

So: when I started my frequency research as an amateur and sporadically in 2000, I did not yet know that this frequency plays a fundamental role in anthroposophy. I knew Rudolf Steiner and many of his books, I knew Demeter’s biodynamic foods, I knew a few anthroposophists, but I never associated Steiner with music.

432 Hz was introduced to me by   Ioannes Peregrinus .
His hurdy-gurdy, turning in just intonation, became the guiding principle of my musical activity.

At first! But everything is always in motion and I soon found out more about the frequencies. 432 Hz was not at all the measure of all healing music.

I can’t remember exactly how I came up with it, maybe intuition, but maybe also sufficient knowledge of mathematics and a self-made Excel spreadsheet. That was in 2013.

Octaving

I had simply started at 1 Hz. In the octave series there is also 128 Hz (1-2-4-8-16-32-64-128…). In connection with pure tuning and the natural overtone series, I found a tuning system that I later called Natural Tuning .

Maria Renold

It wasn’t until 2018 that I discovered Maria Renold’s book: „Of Intervals, Scales, Tones and the Concert Pitch C = 128 Hertz“. I understood Maria Renold immediately and was able to understand her work.

However, while the  Maria Renold tuning  is  a tuning system for the analog piano, with which all 12 major scales can be stepped through (similar to the Pythagorean tuning) ,  the universal frequency model of the naturally pure tuning –  natural  tuning – has a different approach.

This is about the pure intonation, which is not consistent in the Maria Renold intonation.

There is a kinship whereby the universal frequency model can include all frequencies and can provide a reference frequency for a scale. That’s not possible with the Maria Ronald mood and that wasn’t the goal either.

But the base frequency is the same, there is the same starting point, there is a reference to the natural tone overtone series.

What is a concert pitch anyway? There are plenty of explanations on the web.
I liked this one the best. Unfortunately I couldn’t find the author anymore.

Pitch in early music

Our current pitch of a = 440 Hertz is a relatively recent achievement. It was determined at a voice tone conference in 1939. Radio orchestras went up to 445-446 Hz in the 1950s and 1970s because of alleged interference in medium and shortwave transmissions. Since the days of VHF and digital radio, this has no longer been an issue, and the cultural orchestras (and with them opera houses, music academies, music schools, concert halls, churches, etc.) settled down to 442 – 443 Hz.

Before 1939, a = 435 was common in many places. Many harmonium instruments from that time still bear witness to this today… Allegedly, Verdi tried to prevent performances of his operas in houses that pitched higher than 435. The tuning pitch 435 gradually became established in the 19th century. But now in order:

High Renaissance:

Up to the year 1600, the question of the pitch of the voice was extremely confusing, since it was handled very differently from region to region. The approach was very pragmatic and undogmatic: the stringed instruments were considered to be very flexible (the instrumentalists had to know for themselves where the string-breaking limit was), trombones and (slide) trumpeters could transpose chromatically, cornetto players and woodwinds had in Usually there are several instruments in all possible tunings. 

Singers liked to sing low, and the notation had a special keying system (chiavettes) that indicated a “rather low” register, deviating from the standard keying, which indicated a high pitch (if at all, then based on the organ tuning tone as a fixed quantity). . 

In case of doubt, organs were tuned rather high, which made them a little cheaper (less material) to manufacture. The difference between the „Cornette tone“ (high) and the then (!!!) choral tone (low) was usually a minor or major third, sometimes (especially when instruments were used) a fourth, according to Praetorius in Italy up to a fifth. 

The organs were quite different, for the most part the a was at least a semitone higher than ours today, i.e. from 465 Hz upwards.

early baroque:

With the period of thorough bass, at least regionally more or less uniform voice tones were established. In Venice and in the German-speaking area at about a = 465-476 Hz (a good semitone higher than today), in Rome and Florence at about 435, in Naples even lower. In France, in the course of the 17th century, a tuning tone of 392 Hz (i.e. 1 whole tone below today’s a) was developed.
Funnily enough, the tradition of transposing in Chiavetta notation continued for a while. For example, For example, Heinrich Schütz wrote his “Musicalische Exequien” in 1636 for the choir in Chiavette in A minor, but for the continuo in E minor. The choir had to transpose according to old custom.

High and late baroque:

After 1700, the sound of French instruments became popular in Germany (i.e. the “Hautbois” = oboe instead of the shawm, the “Flûte traversière” = transverse flute instead of the recorder and the “Basson” = bassoon instead of the dulcian). The voice pitches between Germany and France were a minor third apart (see above). In order to be able to integrate the low French instruments, one occasionally wrote in several keys at the same time: some works from this period therefore have bassoon parts or oboe parts in B flat major, while all other instruments played in G major.

Of course, this was not a sustainable solution. In the end, the French instruments were built on a smaller scale and from about 1715 the tuning tone was shifted down a whole step, ie in Lepzig, for example, from 470 Hz (slightly higher than our b‘) to 421 Hz (slightly higher than our a‘). The stringed instruments were accordingly re-stringed / re-tuned. 

The organs (too complex) and trumpets (metal was incredibly expensive) could not be converted. So the organs continued to be transposed (all Weimar and Leipzig Bach cantatas have organ parts that are a whole tone lower than the rest) and the trumpets were rededicated: C trumpets became D trumpets (hence the large proportion of D trumpet literature in the Baroque period). ). One now speaks of the choral tone (which is now the high one!) for the organs and the concert pitch for the other instruments.

[Note: When historical performance practice emerged in the 20th century, for pragmatic reasons, most ensembles did not tune the Leipzig concert pitch of 421 Hz, which is correct for Bach’s music, but the nearby 415 Hz, which is conveniently exactly one semitone below our contemporary concert pitch. A pragmatism that B. explained from the shifting mechanism on organs and harpsichords. This resulted in the widespread association: „Early music = a semitone lower“.]

Classic and Romantic:

Probably due to the influence of Italian musicians after 1750, especially in Vienna and Munich, the concert pitch in the German-speaking world rose to about 430 Hz (Mozart era), and with the higher-faster-further aesthetics of industrialization in the 19th century gradually to 435 and Furthermore.

Today, 440 Hz is the norm.
But the concert pitch as such is not nearly as important as is commonly believed.
It’s really just an aid in unifying tuning when multiple instruments are playing together.
More important are the intervals that build on the reference frequency .