Universal Yoga
Natural Tuning begins with 1 Hz

Natural Tuning consists of the pitch reference frequency and of pure intervals, whose frequency ratios are the quotients of natural numbers.
All is based on the natural overtone series.
Natural Tuning begins with 1 Hz and includes 432 Hz as well as 256 and 440 Hz.
Just (pure) intonation is the only natural interval design and is the heart of Natural Tuning.
Natural Overtone Series
It is called the natural tone series because its tones, at least up to the 16th member, are formed “naturally” without further ado when a fundamental is made to sound on one side.
The name overtone series wants to suggest that the tones, which cause the interval sequence, ascend from the fundamental in a lawful way.
In this series, the vibrations of successive overtones always increase in the same way by the frequency of the fundamental, or in other words, the product of the number of overtone steps and the frequency of the fundamental gives the number of vibrations of the overtone in question……….
For example, the 3rd overtone forms with the second overtone the interval 3:2, that is, the pure fifth…..
The remaining intervals result in the same way, for example, 2:1 = octave, 3:2 = fifth, 4:3 = fourth, 5:4 = natural major, 6:5 = natural minor, 9:8 = major whole tone, 10:9 = minor natural whole tone, 16:15 = natural semitone, 4:1 or 8:2 = double octave, 45:32 = natural augmented fourth….., 64:45 = natural diminished fifth, and so on.
In other words: it is the scale of nature.
The harmonic series is the chord of partials that vibrate simultaneously when a natural tone is played.
The harmonic series is the foundation of all musical scales and tuning systems, because it is the only natural scale.
As soon as a tone sounds, overtones resonate.
This scale does not come from humans, but originates directly from the laws of vibration of nature. It follows a universal wave principle and we are able to hear and experience it.
For example: The natural tone overtone series for the reference frequency of 1 Hertz simply follows the natural numbers 1 2 3 4 5 6 78 9 10 etc.
The natural numbers are the numbers used in counting.
And you usually start counting at 1. That’s what the creator of the natural tone overtone series did. Who was that? God?
1 Hz and 128 Hz are octaves. 2 Hz and 256 Hz is a double octave, etc.
| Hz | Hz | Ratio | Ton | |||
| Grundton | Grundfrequenz | Prime | 1 | 128 | 1:1 | C3 |
| 01. Oberton | doppelte Frequenz | Oktave zum Grundton | 2 | 256 | 2:1 | C4 |
| 02. Oberton | dreifache Frequenz | Quint zum 1.Oberton | 3 | 384 | 3:2 | G4 |
| 03. Oberton | vierfache Frequenz | Quart zum 2.Oberton – Oktave zum 1. Oberton | 4 | 512 | 4:3 | C5 |
| 04. Oberton | fünffache Frequenz | große Terz zum 3. Oberton | 5 | 640 | 5:4 | E5 |
| 05. Oberton | sechsfache Frequenz | kleine Terz zum 4. Oberton | 6 | 768 | 6:5 | G5 |
| 06. Oberton | siebenfache Frequenz | 7 | 896 | 7:6 | Bb5 aus*1 | |
| 07. Oberton | achtfache Frequenz | Oktave vom 3. Oberton – Quart vom 5. Oberton | 8 | 1024 | 8:7 | C6 |
| 08. Oberton | neunfache Frequenz | großer Ganzton zum 7. Oberton | 9 | 1152 | 9:8 | D6 |
| 09. Oberton | zehnfache Frequenz | kleiner Ganzton zum 8. Oberton | 10 | 1208 | 10:9 | E6 |
| 10. Oberton | elffache Frequenz | 11 | 1408 | 11:10 | F6 aus *2 | |
| 11. Oberton | zwölffache Frequenz | Oktave zum 5. Oberton | 12 | 1536 | 12:11 | G6 |
| 12. Oberton | dreizehnfache Frequenz | 13 | 1664 | 13:12 | Ab6 aus *3 | |
| 13. Oberton | vierzehnfache Frequenz | Oktave zum 6. Oberton | 14 | 1792 | 14:13 | Bb6 aus*4 |
| 14. Oberton | fünfzehnfache Frequenz | 15 | 1920 | 15:14 | B6 | |
| 15. Oberton | sechszehnfache Frequenz | kleine Sekunde | 16 | 2048 | 16:15 | C7 |
Und so geht die Reihe nach diesem Muster weiter: 16. Oberton – Ratio 17:16 bis ins Unendliche.
| *1 die Frequenz stammt aus der Tonleiter Bb – Bezugsfrequenz 7 HZ – siebte Oktave |
| *2 die Frequenz stammt aus der Tonleiter F – Bezugsfrequenz 11 HZ – siebte Oktave |
| *3 die Frequenz stammt aus der Tonleiter As – Bezugsfrequenz 13 HZ – siebte Oktave |
| *4 die Frequenz stammt aus der Tonleiter Bb – Bezugsfrequenz 7 HZ – achte Oktave |
| Was fällt auf? Alles B‑Tonleitern. |
| Es werden englische Tonbezeichnungen verwendet. |
Just Intonation
Just intonation or pure intonation is any musical tuning in which the frequencies of notes are related by ratios of natural numbers.
Notes are organized in scales.
A scale consists of the reference frequency and the intervals based on it
Any interval tuned in this way is called a pure or just interval.
The simple-ratio intervals upon which Just Intonation is based are the fundamental constituents of melody and harmony. They are what the human auditory system recognizes as consonance. The significance of whole-number ratios has been recognized by musicians around the world for at least five thousand years.
Just Intonation is not a particular scale, nor is it tied to any particular musical style. It is, rather, a set of principles which can be used to create a virtually infinite variety of intervals, scales, and chords which are applicable to any style of music.
Just intonation was born in Europe in the second half of the 15th century.
Octave and Octavation
256 Hz divided by 2 = 128 Hz
divided by 2 = 64 Hz
divided by 2 = 32 Hz
divided by 2 = 16 Hz
divided by 2 = 8 Hz
divided by 2 = 4 Hz
divided by 2 = 2 Hz
divided by 2 = 1 Hz (1 cycle per second)
1 Hz is the basic reference frequency of Natural Pure Tuning System.
256 Hz is the eighth octave of 1 Hz.
An octave means the doubling of an frequency.
Row of octaves:
0-1-2-4-8-16-32-64-128-256-512-1024-2048-4096-8192-16384-32768 ………
Reference Frequencies
The pitch reference frequencies are always
odd numbers, integral numbers, natural numbers
and bear reference to the traditional 12 keynotes of western scales.
The first reference frequency is 1 Hz.
The second reference frequency is not 2 Hz,
because 2 Hz belongs to the octavation of 1 Hz,
an octave is the same tone…….
3 Hz is the next reference frequency for a pure scale.
4 Hz belongs to the octavation of 1 Hz.
Next is 5 Hz and so on…..
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 27 | 45 |
| C | G | E | Bb | D | F | Ab | B | Db | Eb | A | Gb |
Octavation means Transposition by an octave.
This universal frequency model is called Natural Pure Tuning, it is a natural tuning system, because it is based on the natural harmonic series.
Keynote
C is a symbol, which stands for the first note of a musical scale. C has no information about the real pitch. The frequenz of C is the important thing. We say: C has a frequency reference of 1 HZ. That is precise! The Concert pitch (A4) is 426,67 Hz. Another example: A is the first note. A has a frequency reference of 27 HZ. The Concert pitch (A4) is 432 Hz.
Concert pitch
Concert pitch refers to the pitch reference to which a group of musical instruments are tuned for a performance. Concert pitch may vary from ensemble to ensemble, and has varied widely over musical history. In Natural Pure Tuning the concert pitch varies according to the reference frequency.
Why does Just Intonation sound so good?
There are several reasons for this. First of all our auditory systems find it easier to process simple harmonic information than complex harmonic information. Just Intonation intervals are much easier for our ears to “digest”. For example, a pure major third has the two tones in the ratio of 4:5, whereas a major third in 12 Tone Equal Temperament has them in a ratio which is approximately 504:635.
Our brains tell us that the first interval is more consonant, simply because it requires less effort to process than the second one. Of course, in the real world, things are rarely absolutely perfect and two tones in the ratio of 40001:50001 will be heard as “near enough” to 4:5.
However, the further an interval strays from a nice simple ratio, the harsher it will tend to sound. Intervals that do not form perfect small number ratios with each other produce beats.
universal frequency tuning
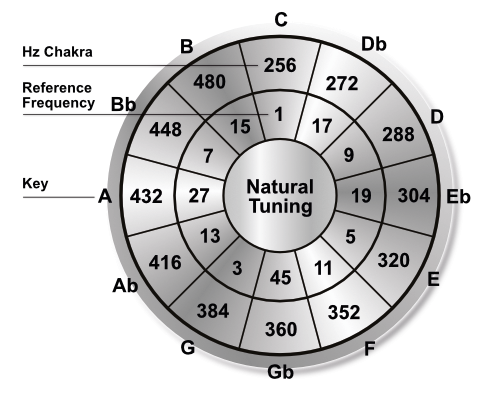
| Reference Frequency | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 27 | 45 |
| Scale | C | G | E | Bb | D | F | Ab | B | Db | Eb | A | Gb |
| Chakra HZ | 256 | 272 | 320 | 448 | 288 | 352 | 416 | 480 | 272 | 304 | 432 | 360 |
Red is the reference frequency of the scale – Blue is the frequency of the chakras
all odd natural numbers are reference frequencies – 1-3-5-7-11-13-17-19……Hz
the root of the scale is called the reference frequency
| Hz | Oktaves | Scale | Concert Pitch A4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C-1 | C0 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |||||
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | C | 426,67 Hz |
| Db-1 | Db0 | Db1 | Db2 | Db3 | Db4 | Db5 | Db6 | Db7 | Db8 | |||||
| 1,0625 | 2,125 | 4,25 | 8,5 | 17 | 34 | 68 | 136 | 272 | 544 | 1088 | 2176 | 4352 | Db | 435,2 Hz |
| D-1 | D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | |||||
| 1,125 | 2,25 | 4,5 | 9 | 18 | 36 | 72 | 144 | 288 | 576 | 1152 | 2304 | 4608 | D | 432 Hz |
| Eb-1 | Eb0 | Eb1 | Eb2 | Eb3 | Eb4 | Eb5 | Eb6 | Eb7 | Eb8 | |||||
| 1,1875 | 2,375 | 4,75 | 9,5 | 19 | 38 | 76 | 152 | 304 | 608 | 1216 | 2432 | 4864 | Eb | 427,5 Hz |
| E-1 | E0 | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | |||||
| 1,25 | 2,5 | 5 | 10 | 20 | 40 | 80 | 160 | 320 | 640 | 1280 | 2560 | 5120 | E | 426,67 Hz |
| F-1 | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | |||||
| 1,375 | 2,75 | 5,5 | 11 | 22 | 44 | 88 | 176 | 352 | 704 | 1408 | 2816 | 5632 | F | 440 Hz |
| F#-1 | F#0 | F#1 | F#2 | F#3 | F#4 | F#5 | F#6 | F#7 | F#8 | |||||
| 1,40625 | 2,8125 | 5,625 | 11,25 | 22,5 | 45 | 90 | 180 | 360 | 720 | 1440 | 2880 | 5760 | Gb | 432 Hz |
| G-1 | G0 | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | |||||
| 1,5 | 3 | 6 | 12 | 24 | 48 | 96 | 192 | 384 | 768 | 1536 | 3072 | 6144 | G | 432 Hz |
| Ab-1 | Ab0 | Ab1 | Ab2 | Ab3 | Ab4 | Ab5 | Ab6 | Ab7 | Ab8 | |||||
| 1,625 | 3,25 | 6,5 | 13 | 26 | 52 | 104 | 208 | 416 | 832 | 1664 | 3328 | 6656 | Ab | 443,73 Hz |
| A-1 | A0 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |||||
| 1,6875 | 3,375 | 6,75 | 13,5 | 27 | 54 | 108 | 216 | 432 | 864 | 1728 | 3456 | 6912 | A | 432 Hz |
| Bb-1 | Bb0 | Bb1 | Bb2 | Bb3 | Bb4 | Bb5 | Bb6 | Bb7 | Bb8 | |||||
| 1,75 | 3,5 | 7 | 14 | 28 | 56 | 112 | 224 | 448 | 896 | 1792 | 3584 | 7168 | Bb | 420 Hz |
| B-1 | B0 | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | |||||
| 1,875 | 3,75 | 7,5 | 15 | 30 | 60 | 120 | 240 | 480 | 960 | 1920 | 3840 | 7680 | B | 432 Hz |
Wikipedia Links
